Gershgorin Circle Theorem Visualization

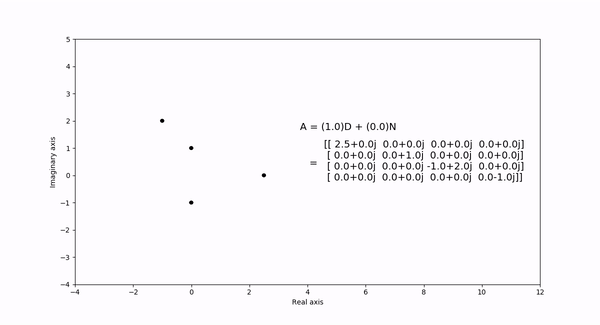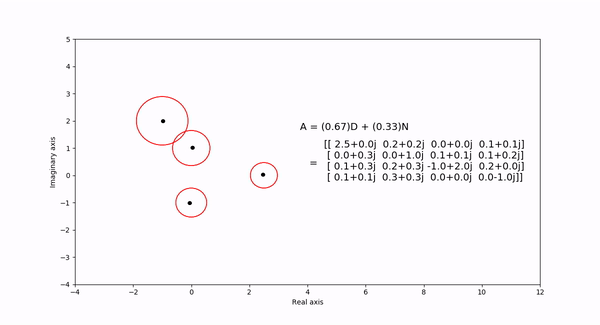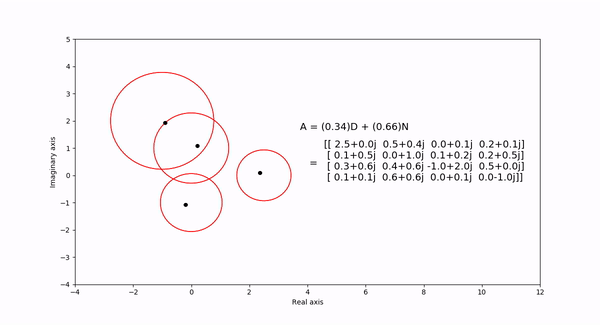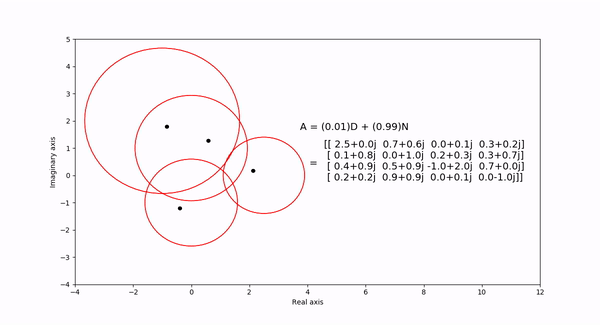
The Gershgorin circle theorem bounds the eigenvalues of a square matrix within Gershgorin discs. Each disc is a circle centered at the \(ith\) diagonal element with radius equal to the sum of the absolute values of the \(ith\) row elements. In the following visualization, the eigenvalues and discs of matrix \(A = (1-t)D + tN\) are shown as the eigenvalues are continuous in \(t\) as it varies from 1 to 0. \(D\) is a diagonal matrix entries equal to the diagaonal elements of \(N\).